VARIOUS
MATRIX FORMALISM TO DESIGN ION LINEAR ACCELERATORS
V.A.Moiseev, S.E.Bragin, INR of RAS,
The well-known betatron
function parameterization in the beam optical computations provides an
emittance independent representation of the properties of a beam transport
system. The acceleration effects lead to nonsymplecticity of the transfer
matrix. The error analysis of matrix presentation in the different phase spaces
has been carried out. The coupling transformations of betatron functions for
the studied phase spaces are presented.
INTRODUCTION
The traditional betatron functions 
and 
(the betatron phase
advance) are widely used to design the beam transport systems without
acceleration [1]. They permit to decouple the problem of matching the
characteristics of the injected beam to the acceptance of a transport system.
However, the application of standard symplectic matrix mapping becomes
unreliable when the acceleration effects are included. This effect depends from
the choice of a phase space to design the beam transport system. Mainly this
problem is important for the linear particle accelerators, where the
accelerating parts are larger then parts without acceleration.
Formally,
the single particle motion is described in a 6 – dimensional phase
space. For simplicity we will restrict consideration to decoupled nondispersive
beam transport systems, where the single particle dynamics for any direction is
presented by 
matrix. Therefore further only one transverse direction will
be under study.
GENERAL
FORMALISM
On the whole for any phase space the linear particle dynamics from
longitudinal point 
to 
of a transport system
may be described by matrix
, (1)
where 
is the transverse
coordinate and 
is the second phase
space coordinate. In general the determinant of (1)
(2)
may be not equal unity. In this case the
transformation (1) will be nonsymplectic and beam emittance [1] will be not
conserved. At position 
in a transport line
all beam particles lie within the ellipse [1]
, (3)
where 
is the beam emittance.
According (1)
the phase space particle dynamics between positions and is described by
. (4)
Applying (3) for two mentioned above points and
introducing the definitions
, 
, 
, (5)
the following expressions for the betatron function
propagation may be derived
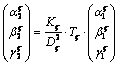, (6)
where 
, and matrix 
has the standard form like for a beam transport system
without acceleration [1]:
.
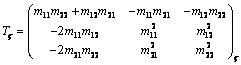From (6) it is possible to get the followed coupling
coefficient for the betatron functions at different points of a beam transport
system
. (7)
Whence it follows that for the arbitrary chosen phase
space coordinates the next condition may be valid
. (8)
CANONICAL
PHASE SPACE
The canonical-conjugated variables are the coordinate and momentum 
[1] for any transverse direction. For this
phase space the beam emittance is an invariant [1]. Further the modified momentum is used:
, (9)
where 
is a transverse
particle velocity; 
is the light velocity;
is a particle
relativistic factor. In the formulas from previous section replacing 
the following
equalities are valid for the canonical phase space [1]:
; 
; 
; 
. (10)
The matrix 
is symplectic and the
beam emittance is invariant for the beam phase space motion [1]. Defining the
betatron phase advance between positions and as
, (11)
the elements of matrix may be calculated [2]:
(12)
.
And if the matrix elements are calculated by any way,
the betatron function propagation (6) will be
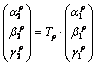(13)
and
. (14)
The beam phase space ellipse (3) will be governed by
(15)
The above formalism is valid for Hamiltonian systems
including both a beam transport system without acceleration and with
acceleration [1]. However the exact matrix description in the canonical phase
space for the accelerating
beam transport systems is difficult and has not a wide practice application.
NONCANONICAL
PHASE SPACES
Standard Phase Space
The traditional representation of
the beam transport systems is based on a noncanonical phase space 
, where the angular divergence 
is determined as
, (16)
here 
is the modified
canonical momentum (9) and 
is the modified
longitudinal momentum of the synchronous particle at a point of observation.
Using (16) the coupling relations between the matrices and 
are:
, 
,
, 
.
Taking into account (10) it follows that
; 
; 
. (17)
From (17) it results that:
·
matrix
is nonsymplectic and
its determinant is reduced in an
accelerating transport system, hence it does not admit a representation by
(12)÷(14);
·
the
beam emittance 
is ”adiabatically damped”
along a transport system with acceleration;
·
the
coupling coefficient (8) 
is the constant
of motion.
If the matrix elements are calculated by any way, the
betatron function propagation (6) will be
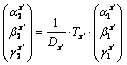. (18)
To calculate the betatron phase advance (11) the
general definition [1] may be used
. (19)
The beam phase space ellipse (3) in the phase space
studied will be governed by
. (20)
Comparing (20) and (15) the following betatron
function coupling for the phase spaces and is
; 
; (21)
; 
.
From (10), (17) and (21) it follows that the coupling
coefficient invariant is
. (22)
Basing on the geometric characteristics of a phase
ellipse [1], the real beam parameters at the fixed longitudinal point of a
transport system are:
spot size 
;
divergence 
.
Because of the betatron phase advance must be
independent of the presentation chosen to describe the beam motion [2] the
followed expression is valid
. (23)
The
presented matrix formalism permits to simulate exactly the betatron function
propagation in a beam transport system with acceleration if the matrix was qualitatively
determined. For example, the accelerating element models from [3] may be used.
Note, the
equation (18) is coincided with the results of paper [2], but the algorithm
presented in this paragraph is simpler and demands less number of the
calculations.
Modified Phase Space
To study a beam transport system with acceleration the modified phase
space 
, where 
is the transverse
particle velocity (9), was proposed. The
independent variable is the time. Further the time markers 
and 
will be the moments when the synchronous particle traverses
the longitudinal points and .
Applying
the previous section approach it follows:
, 
, 
, (24)
where 
and 
are the relativistic
factors of the synchronous particle at the moments and respectively. From
(24) it results that:
·
matrix
is nonsymplectic and
its determinant is reduced in an
accelerating transport system, hence it does not admit a representation by
(12)÷(14);
·
and 
for 
;
·
the
beam emittance 
is ”adiabatically damped” along a transport system with
acceleration;
·
the
coupling coefficient (8) 
is the constant of
motion.
The coupling relations between the matrices and are:
, 
, 
.
The betatron function propagation is governed by
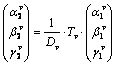. (25)
The betatron function parameterization (3) in the
phase space is
. (26)
The betatron function coupling for the phase spaces and is:
; 
; 
. (27)
Therefore the coupling coefficient invariant is
. (28)
There is simple equality for the betatron phase
advance (11) in the and phase spaces:
. (29)
The real beam parameters at fixed time moment 
corresponding to the longitudinal point of a transport system
are:
;
.
PRACTICAL
APPLICATION
Assuming the qualified presentation of matrices , and , the algorithms
presented above permit to get the reliable results of the desired betatron
function propagation in a designed beam transport system even with the
accelerating elements. In practice the accelerating elements are presented by
the simplified models. For example, the proposed method [2] to propagate the
betatron functions is complicated and used the “poor” rf-resonator model. In
this case the calculation errors may be undesirable large. The widespread and
more simple methods (for example [3]) exist to constrain a transfer matrix 
or 
for a noncanonical
phase space with the determinants
and 
; 
and 
. (30)
The basic
elements of a linear accelerator structure are the periodic parts with acceleration
and transverse focusing (main parts), and matching sections for the different
accelerator periodic parts. As a rule the beam energy gain both for the
matching parts and main parts is insignificant compared with the beam energy.
Therefore an application of the models with (30) may be effective in spite of
the violations for some conditions (17) or (24).
On the
base of the modified phase space the program complex was developed to design
and simulate both the matching and periodic parts of the ion linear
accelerators using the conditions (30). This complex was applied to match some
periodic parts of the INR Linac [4]. In the Table 1 some parameters and
determinants of the models are presented for two first matching parts of the
INR Linac:
Table 1: Noncanonical
Determinants
|
¹ |
Input
energy, MeV |
Output
energy, MeV |
|
|
|
1 |
100.1 |
113.3 |
0.937 |
0.987 |
|
2 |
139.3 |
158.6 |
0.933 |
0.982 |
Obviously to use for the simulation the modified phase
space with (30) is more reliable from point of view to reduce the expected
errors. For the periodic parts of the INR Linac the beam energy gain is
~3.7 MeV per period. It means that in the phase space the beam transfer
matrices are very close to condition (30), which leads to possibility to use
the mathematical formalism (12)÷ (14).
CONCLUSIONS
The betatron function matrix formalism for the accelerating transport
systems has been studied both for the canonical and noncanonical phase spaces.
The exact formulas for the betatron function propagation are presented for all
phase spaces studied. It was shown that the modeling of an ion accelerator in
the phase space does not create the additional
problems for the matrix description of the standard elements of a beam
transport system. Moreover for the low and medium beam energy ranges it permits
to get a reliable solution for the betatron function propagation in an
accelerating transport system by using the standard canonical matrix formalism.
REFERENCES
[1] E.Keil, “Single-particle
dynamics – linear theory of perfect machines”, “Single-particle dynamics –
linear machine lattices”, Theoretical aspects of the behaviour of beams in
accelerators and storage rings,
[2] D.R.Douglas,
J.Kewisch, R.C.York, “Betatron Function Parameterization of Beam Optics
Including Acceleration”, LINAC’88, CEBAF-Report-89-001,
[3] K.R.Crandall, “Trace-3D
documentation”, LA-11054-MS,
[4]
S.E.Bragin et. al., “Transverse Beam Matching and Correction Procedures in INR
LINAC”, LINAC’06, Knoxville, USA, p. 435 (2006); http://www.JACoW.org.